Multiplication of any number with 11

H.D. Motiramani

11 as the number suggests, has a double 1 that is 1 on 1, 11. Surprisingly, multiplication of 11 with other single digit number also results into single digit multiples. For example 2×11 = 22, 3×11 = 33 and so on.

Multiplication of any number having more than one digit is also very simple. The method is nothing but   a successive addition technique. This will become clear through the examples below:

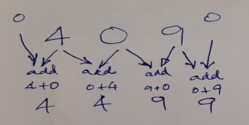Suppose a number 409 is to be multiplied by 11. What we need to do is put an imaginary zero on both sides of the number 409. Then starting from right, add the right most zero to the unit digit 9. In next operation, the unit digit 9 needs to be added to the digit at tenth place that is 0. Thereafter this 0 is to be added to its left side digit 4. Lastly the digit 4 is added to imaginary zero or put as it is. That makes the answer 4499. Let us see some more examples:

Example   418 to be multiplied by 11:

Let this number be imagined like °418° that is imaginary zeros on both left and right digits.

Right most imaginary zero on top is added to 8.  So 0+8=8, no carry over                                                    °4 1 (8+0)

Next comes the digit 8 which is added to its left side adjacent digit 1. So 8+1=9, no carryover                      °4 (1+ 8)

Next digit is 1. This is added to its left adjacent digit 4 so 1+4=5, no carryover                                           °(4 + 1)

Next remains the leftmost digit 4 which is now added to imaginary zero on its top left so 4+0=4                    (0+4)

So the answer becomes 4598

Example   2589 to be multiplied by 11:

Let this number be imagined as °2589°

Right most imaginary zero is to be added to 9. So 0+9=9, no carryover                                                          °258 (9+0)

Now the digit 9 needs to be added to its adjacent digit 8. So 8+9 = 17, carryover is 1                                     °25(8 +9)

Now 5 when added to 8 makes it 13 but this 13 needs to add the carry from 17 so 13+1 = 14 , carryover is 1 2(5+8+1)

Now 2 is added to 5 to make it 7, to it is added carryover of previous step thus 7+1=8                                    ⁰(2+5 +1)

There is an imaginary 0 on left which needs addition to its neighboring digit. So 0+2 =2                                          (0+2)

So the answer becomes 28479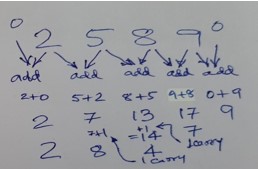

The last example involving carryover is supported with a figure.

—00—

< Contents